Определение 8.4.3.1. Поверхность, имеющая уравнение 
(8.7.) где p > 0, q > 0 называется эллиптическим параболоидом.
1) Если p=q, то эллиптический параболоид будет поверхностью вращения, образованный вращением параболы 
вокруг оси z.
2) В общем случае 
эллиптический параболоид не является поверхностью вращения: сечения его плоскостями перпендикулярными оси z, уже не окружности ,а эллипсы.
Доказано, сечения эллиптического параболоида плоскостями, параллельными плоскости ху, задаются системой уравнений 
. Так как p и q>0, то 
при любых значениях x и y.
1) Если h < 0, то эта система не имеет решений, т.к. 
. Поэтому «под плоскостью» ху нет точек эллиптического параболоида.
2) При h = 0 система имеет единственное решение (0; 0; 0), т.е. эллиптический параболоид имеет с плоскостью ху единственную общуюточку - начало координат.
3) При h > 0 система определяет эллипс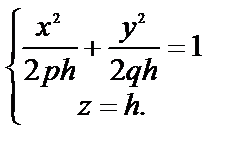 
, с полуосями
. При возрастании h полуоси эллипса возрастают (неограниченно).
Сечение эллиптического параболоида координатными плоскостями xz и yz представляют собой параболы, которые задаются соответственно системами уравнений: 
и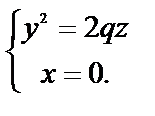 
Если в уравнении (8.7.) p=q , то в сечениях горизонтальными плоскостями образуются окружности.
Замечание. Уравнения 
и 
также определяют эллиптический параболоид.
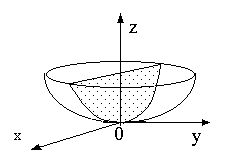
Рис.8.12.
