Цилиндром второго порядка называется цилиндрическая поверхность, направляющей которой является эллипс (окружность), гипербола или парабола (т.е. кривые второго порядка).
К цилиндрам второго порядка относятся эллиптический цилиндр, гиперболический цилиндр и параболический цилиндр.
Уравнение 
определяет в плоскости Oxy эллипс, а в пространстве - определяет цилиндрическую поверхность с образующими, параллельными оси Oz и пересекающуюся с плоскостью Oxy по этому эллипсу. Такая поверхность называется эллиптическим цилиндром. (Рис.8.2.). Заметим, что название цилиндрической поверхности определяется названием направляющей. Уравнение 
в пространстве трех переменных определяет круговой цилиндр с образующими, параллельными оси OZ.
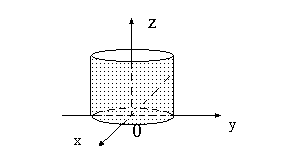
Рис.8.2.
Гиперболический цилиндр - определяется уравнением: 
(Рис.8.3.)
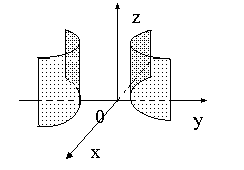
Рис.8.3.
Параболический цилиндр - определяется уравнениями:
или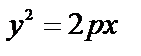 
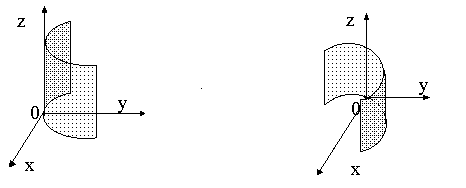
Рис.8.4. Рис.8.5.
