Определение 7.4.1. Параболой называется множество точек плоскости равноудаленных от данной точки называемой фокусом и данной прямой называемой директрисой.
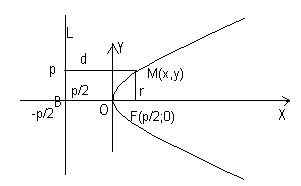
Рис.7.4.
Пусть Р — расстояние (большее нуля) от фокуса F до директрисы l. Ось 0x выберем так чтобы она проходила через F перпендикулярно l. Начало координат поместим в середине отрезка  , где B точка пересечения оси 0x и директрисы l. В выбранной системе координат уравнение директрисы
, где B точка пересечения оси 0x и директрисы l. В выбранной системе координат уравнение директрисы  . Расстояние P называется параметром параболы.
. Расстояние P называется параметром параболы.
Согласно определению
 или
или 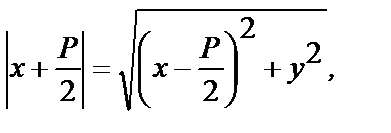
освободимся от иррациональности:

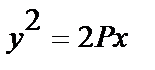 (7.4.)
(7.4.)
— каноническое уравнение параболы.
Ось, на которой расположен фокус, называется фокальной осью.
Уравнение параболы, симметричной относительно оси Oy и проходящей через начало координат имеет вид:  , где
, где  - ее директриса.
- ее директриса.
Эксцентриситет параболы:  .
.
Уравнение касательной проходит через точку (x0,y0):  .
.
Пример 7.4.1. Составить уравнение параболы, проходящей через точки пересечения прямой  с окружностью
с окружностью  и симметричной относительно оси 0x.
и симметричной относительно оси 0x.
Решение: Найдем точки пересечения прямой с окружностью
 , Ы
, Ы 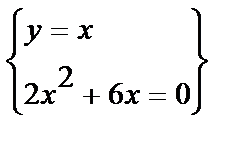 Ы
Ы 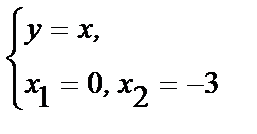
 Найдем значение p:
Найдем значение p:

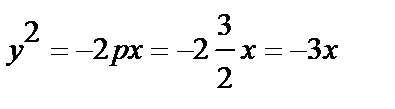
Ответ.  .
.