Определение 7.3.1. Гиперболой называется геометрическое место точек плоскости, модуль разности расстояний каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная равная 2а. (Рис.7.2.)
Рис.7.2.
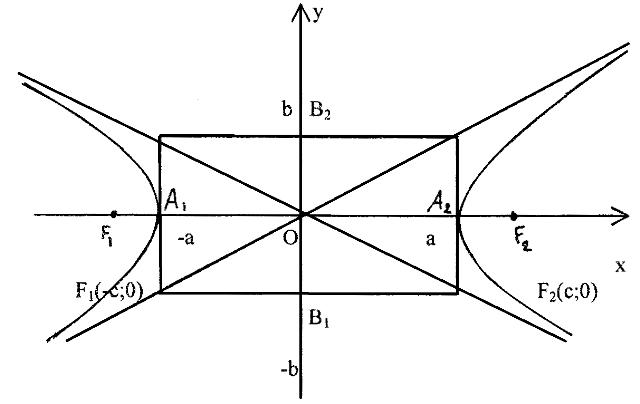
Рис.7.3.
Точки F1(-c;0) , F2(c;0) называются фокусами гиперболы. Точки A1и A2называются действительными вершинами гиперболы. Точки B1и B2– мнимыми вершинами. Точка O(0;0) называется центром гиперболы.
Найдем r1 и r2 и подставим в равенство:
произведем преобразования аналогично в (7.2.)
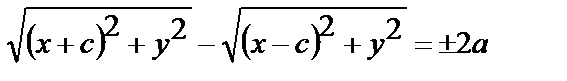
Полагая 
.
Получим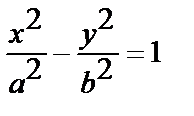 
(7.3.) — называется каноническим уравнением гиперболы.
Прямые, на которых лежат диагонали прямоугольника, являются асимптотами гиперболы. Их уравнения: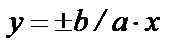 
Эксцентриситет гиперболы характеризует форму основного прямоугольника и форму самой гиперболы, он равен 
.
Прямые 
и 
параллельные малой оси гиперболы и отстоящие от нее на расстоянии равной 
называются директрисами гиперболы. Уравнения директрис: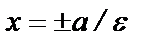 
.
Фокальные радиусы точки M (правой) : 
, 
,
левой точки 
: 
, 
.
Если фокусы гиперболы расположены на оси OY , то ее уравнение
имеет вид: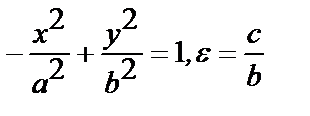 
Касательная в точке 
имеет уравнение : 
.
Пример 7.3.1. Гипербола проходит через точку 
, ее фокусы находятся в точках 
и 
. Составить уравнение ее асимптот и найти угол между ними.
Решение. 
, 
Ю 
.
Уравнение асимптот 
.
Угол 
- угол между двумя прямыми, угловые коэффициенты их равны: 
, 
Ю применим формулу:
Ю 
Ю 
.
