Пусть в R3даны прямая l и плоскость a:
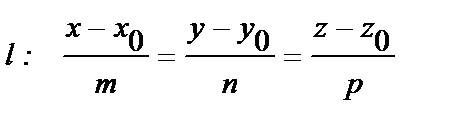
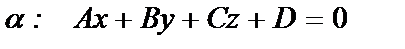
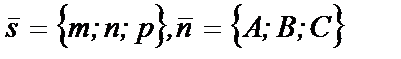
Выясним условия параллельности и перппендикулярности прямой и плоскости, опираясь на взаимное расположение вектора нормали и направляющего вектора прямой.
Если прямая и плоскость параллельны (см. Рис.6.11.), то 
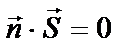
В координатной форме: 
(6.31.)
Если прямая l и плоскость a перпендикулярны (см.Рис.6.12.), то 
коллинеарные 
(6.32.)
Условия (6.31.) и (6.32.) называются соответственно условиями параллельности и перпендикулярности прямой и плоскости.
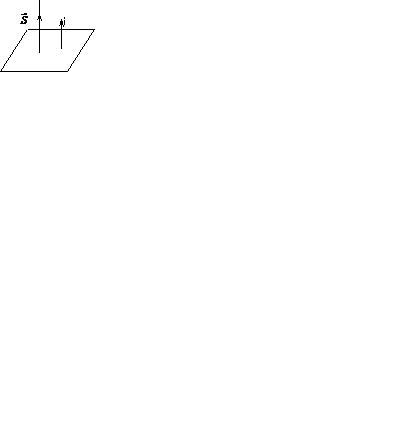
Рис.6.11. Рис.6.12.
Пример 6.4.2. Доказать, что прямая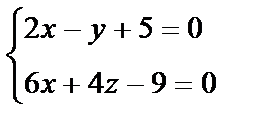 
и плоскость 
параллельны.
Решение: Найдем направляющий вектор прямой: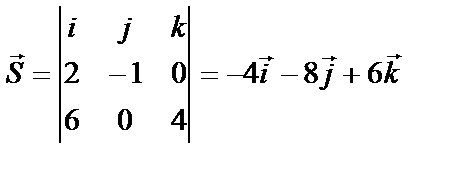 
нормальный вектор плоскости имеет координаты:
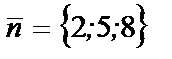
Проверим условие (6.31.) 
.
Ответ: Прямая и плоскость параллельны.
