Для определения взаимного расположения прямой и плоскости в пространстве достаточно установить, параллельна ли прямая lплоскости a или нет. Если нет, то в какой точке пересекает ее и под каким углом.
6.4.1. Пересечение прямой и плоскости в пространстве R3
Пусть в пространстве R3 даны своими уравнениями прямая l и плоскость a:
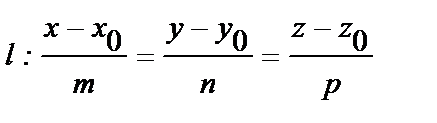
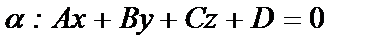
Определим точку пересечения прямой с плоскостью. Перейдем к параметрическому виду задания прямойl:
 ,
,  ,
,  (6.30.)
(6.30.)
Найдем значение t соответствующее точке пересечения прямой и плоскости. Так как по условию прямая пересекает плоскость, то 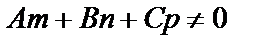
(6.30.) подставим в уравнение плоскости, найдем параметр t для точки пересечения по формуле:
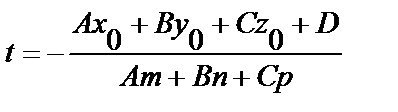 .
.
Подставив t в каждое из уравнений (6.30.) получим координаты искомой точки.
Пример 6.4.1. Найти точку пересечения прямой  с плоскостью
с плоскостью  .
.
Решение: Перейдем от канонического задания прямой к параметрической форме; подставим x,y,z в уравнение плоскости и найдем t:
 ,
,  ,
,  ,
,  .
.
Подставим t в параметрическое уравнение:
 .
.
Ответ: M(16;37;34).