Всякие две пересекающиеся плоскости 
и 
заданные уравнениями:
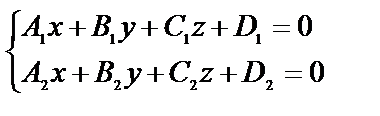(6.26.)
определяют линию их пересечения.
Уравнения (6.26.) называют общими уравнениями прямой. Если плоскость 
непараллельна плоскости 
то :Ю 
.
Чтобы из (6.26.) получить каноническое уравнение надо найти: 1) точку, удовлетворяющую одновременно двум уравнениям; 2) направляющий вектор 
.
Найдем точку, удовлетворяющую уравнениям (6.26.), из системы найдется определитель не равный нулю:
Пусть 
то (6.26.) записываем в виде:
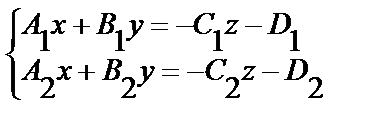
Пусть 
. Решив данную систему находим 
, 
.Любой вектор лежащий на прямой перпендикулярен нормалям плоскостей ,
, т.е.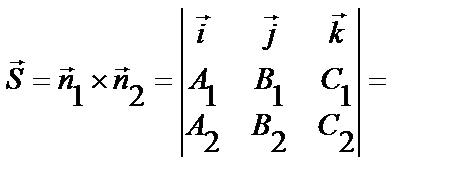 
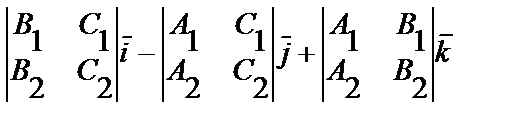
Отсюда каноническое уравнение имеет вид
.
Пример 6.3.1. Составить каноническое уравнение прямой
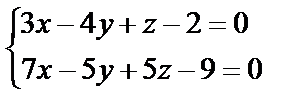
Решение: Найдите точку 
, удовлетворяющую данной системе:
1) Положив 
, 
, Решив систему получим: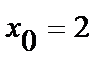 
, 
.
Точка 
. Координаты нормальных векторов заданных плоскостей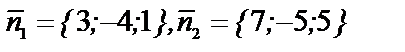 
. Найдем направляющий вектор прямой:
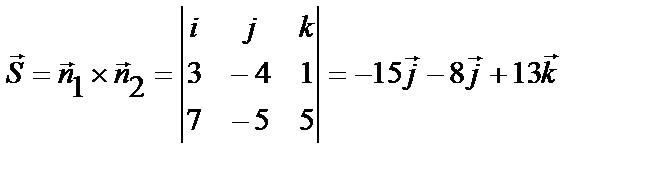
Подставим найденные величины в уравнение (6.24.).
Следовательно каноническое уравнение имеет вид:
.
