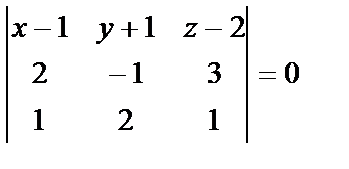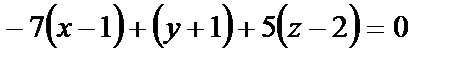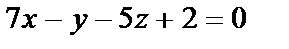Пусть в пространстве R3 даны три точки не лежащие на одной прямой. Выберем в этом пространстве произвольную точку M(x,y,z) и построим три вектора: 
.
Рис 6.8.
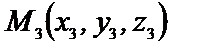
Рассмотрим: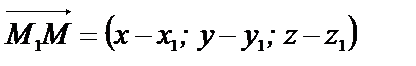 
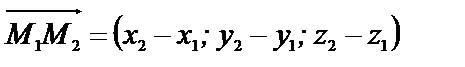
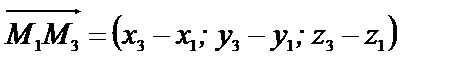
Эти векторы компланарны, поэтому их смешанное произведение равно нулю.
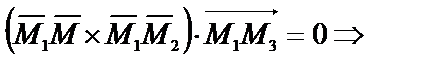или в координатной форме:
(6.17.)
Называется уравнением плоскости проходящей через три точки.
Пример 6.2.2. Составить уравнение плоскости, проходящей через точку 
перпендикулярно плоскостям 
, 
.
Решение : Запишем координаты нормальных векторов данных плоскостей 
Возьмем произвольную точку N(x,y,z), принадлежащую искомой плоскости, тогда координаты вектора 
. Вектора 
, 
и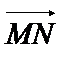 
компланарны. Условие компланарности в координатной форме определит уравнение плоскости:
