Пусть в пространстве с заданной прямоугольной системой координат задан ненулевой вектор 
(см. Рис.5.5.).
z
M
γ
β
O y
α
Рис.5.5.
Направление вектора в пространстве определяется углами 
, которые вектор составляет с осями координат. Косинусы этих углов называются направляющими .
Если вектор 
задан координатами 
={x;y;z} или 
,
где 
- орты координатных осей, то x,y,zявляются проекциями вектора 
на координатные оси OX, OY, OZ в соответствии с теоремой 5.1.1. получим следующие равенства:
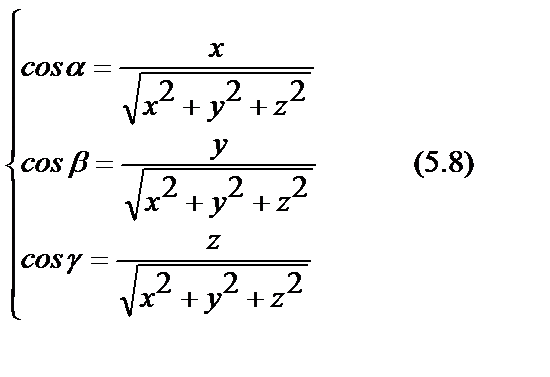
Возведем обе части соотношений (5.8.) в квадрат и сложим, получим: 
.
Сумма квадратов направляющих косинусов любого вектора равна единице.
Для единичного вектора
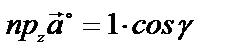
разложение его по осям координат имеет вид: 
.
Пример 5.6.1. На точку действуют три силы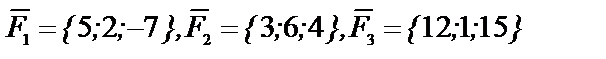 
Найти величину и направление равнодействующей силы 
.
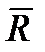Решение: Так как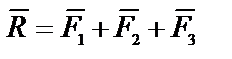 
то R={20,9,12} тогда величи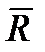на равна 
а ее направление определяется направляющими косинусами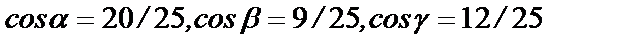 
Контрольные вопросы и задания.
1. Запишите условие коллениарности векторов.
2. Дайте определение скалярного произведения.
3. Перечислите свойства скалярного произведения.
4. Что определяют направляющие косинусы вектора?
5. Какому условию должны удовлетворять ненулевые векторы и 
, чтобы вектор 
был ортоганален вектору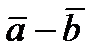 
?
6. Доказать, что скалярное произведение двух векторов не изменится, если к одному из них прибавить вектор, ортогональный другому сомножителю.
7. Найти величину угла между биссектрисами углов XOY и XOZ.
8. Какая тройка векторов называется правой?
