Поскольку 
то 
(5.4.)
Пусть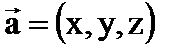 
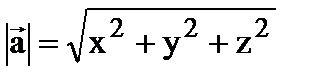(5.5.)
Модуль вектора равен квадратному корню из суммы квадратов его координат .
Если вектор 
задан координатами т.A и т.B 
, то модуль его равен:
(5.6.)
Заметим, что длина вектора равна расстоянию между т. A и т. B.
Пусть даны 
, 
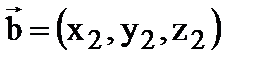
т.к.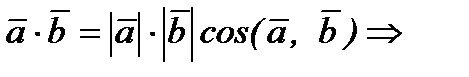 
(5.7.)
Пример 5.5.1. Определите модуль вектора 
?
Решение: Применим формулу (5.5.)
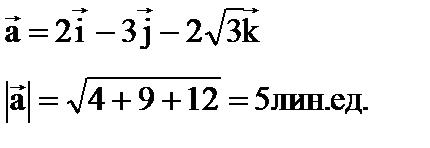
Пример 5.5.2.
Определить длину вектора 
если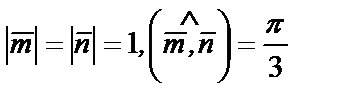 
- угол между векторами 
и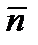 
Решение: применим формулу (5.4.)
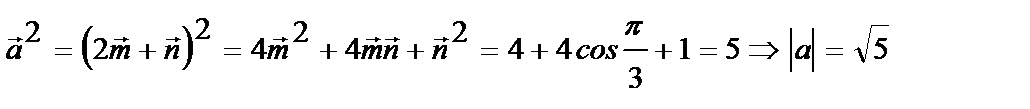
Пример 5.5.3.
Определить угол В треугольника АВС с вершинами
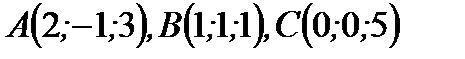
Решение:
Построим треугольник ABC (см. Рис.5.4.) и векторы 
и 
, 
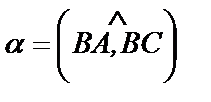
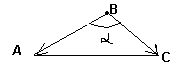
Рис.5.4.
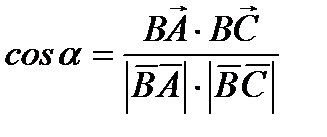
Найдем координаты векторов 
и 
по формуле (5.1.)
, 
найдем по формуле (5.3.)
Применим формулу (5.7.):
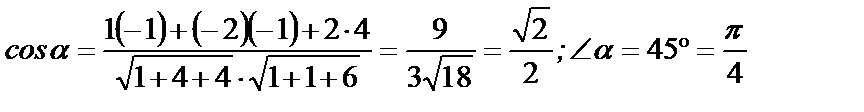
Ответ: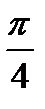 
Пример 5.5.4. Даны три силы 
Найти величину равнодействующей силы R и работу, которую она производит, когда точка M1(0,1,0) ее приложения, двигаясь прямолинейно, перемещается в положение M2(1,0,1).
Решение: Найдем равнодействующую сил 
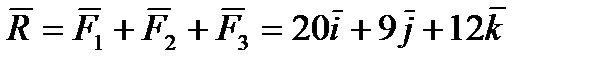, найдем ее величину 
. Искомая работа 
или 
, найдем координаты 
по формуле (5.1.) ={1;-1;1} и по формуле (5.3.): A=20×1+9×(-1)+12×1=23 .
