Определение 5.1.1.
Углом между векторами 
называется наименьший угол
j(0 Јj<p), на который надо повернуть один из векторов до его совпадения со вторым .
Определение 5.1.2.
Под углом между вектором 
и осью l понимают угол j между векторами 
и единичным вектором этой оси .
Теорема 5.1.1.
Проекция вектора 
на ось l равна модулю вектора , умноженному на косинус угла j между вектором и осью .
пр = п пcosj
Доказательство: Рассмотрим треугольник OBB1 : BB1^ OB1
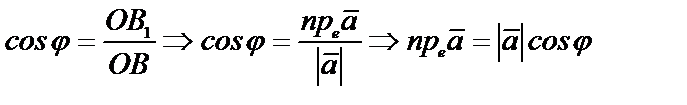
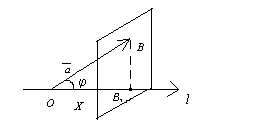
Рис.5.1.
Проекция суммы векторов на какую-нибудь ось равна алгебраической сумме проекций этих векторов на ту же ось.
Определение 5.1.3.
Произведение проекции вектора на ось 
и единичного вектора 
этой оси называется составляющей вектора 
по оси l (см.Рис.5.2.).
Состl 
=прl 
= 
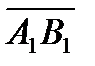
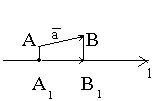
Рис.5.2.
