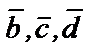Определение 4.3.1.
Пусть W-линейное пространство. Система векторов 
Є W называется базисом линейного пространства W, если :
1) - линейно независима, и
2) 
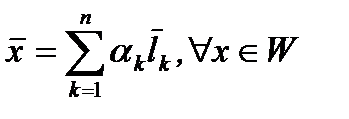
Определение 4.3.2.
Число векторов базиса называется размерностью линейного пространства и обозначается как dimW.
DimV2=2 DimV3=3
В n-мерном пространстве любая линейно независимая система из n-векторов образует его базис , поэтому базисов у линейного пространства существует бесконечно много.
Определение 4.3.3.
Базисом на плоскости называются любые два линейно независимых вектора.Из теоремы 4.2.2. следует, что " два неколлиниарных вектора образуют базис.
Если вектор 
представлен в виде 
, то говорят, что он разложен по базису образованному векторами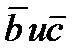 
Определение 4.3.4.
Базисом в трёхмерном пространстве называется три линейно независимых вектора Любой вектор 
однозначно разлагается по векторам 
базиса т.е. выполняется соотношение : 
,
расположен по базису образованному векторами 
