1. При каком значении c система линейных уравнений совместна:
а)  б)
б) 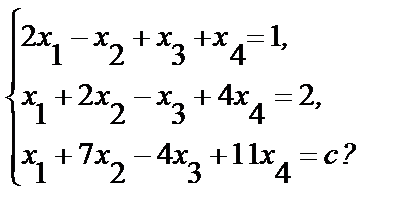
2. Найдите общее решение неоднородной системы линейных уравнений, заданной своей основной матрицей A и столбцом свободных членов B:
а) 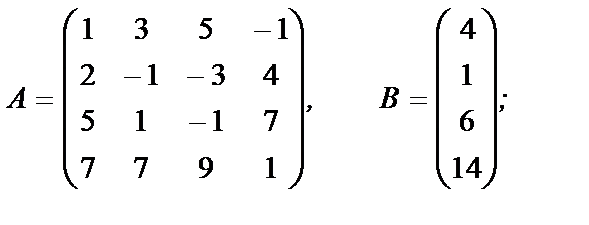
б) 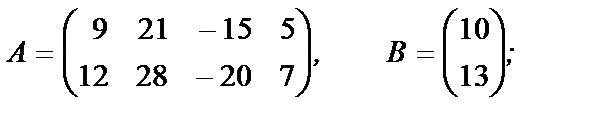
в) 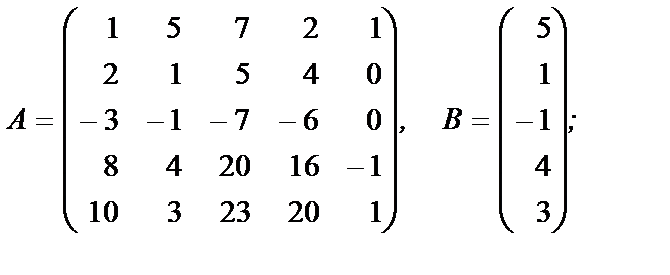
г) 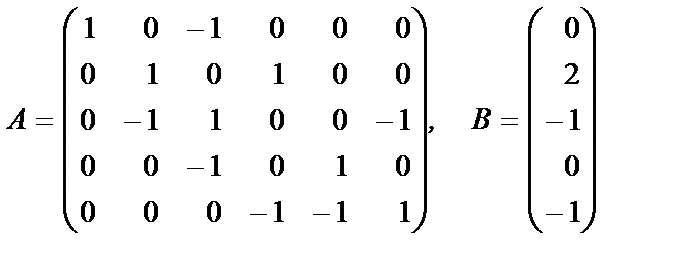
3. Исследуйте на совместимость и найдите общее решение системы:
а)  б)
б) 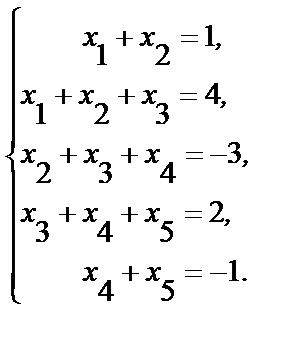
4. Исследуйте систему и найдите общее решение в зависимости от значения параметра c:
а)  б)
б) 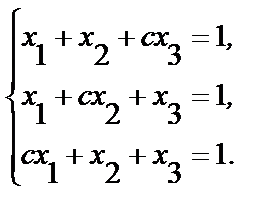
5. Пользуясь методом Гаусса, вычислите решения следующих систем:
1.  2.
2. 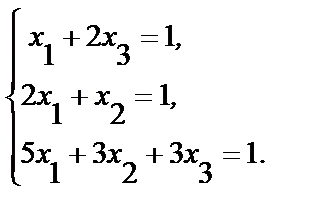
3.  4.
4. 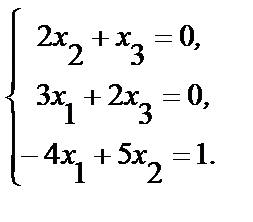
5.  6.
6. 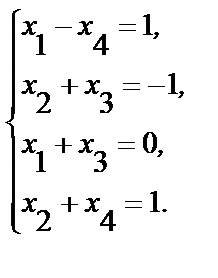
6. Напишите однородную систему линейных уравнений с матрицей:
а)  ; б)
; б)  .
.
7. Найдите общее решение однородной системы линейных уравнений:
а)  б)
б) 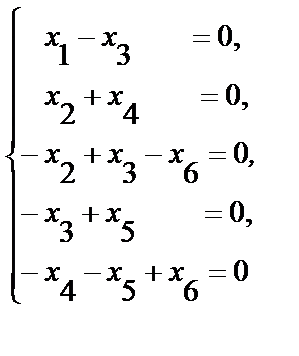
8. Укажите все группы неизвестных, которые могут быть свободными неизвестными системы
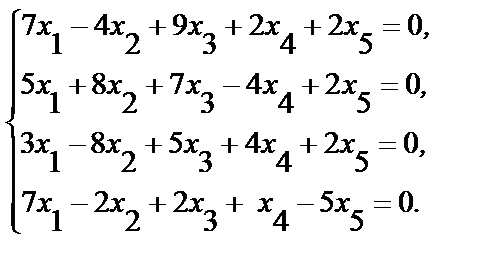
9. Найдите однородную систему линейных уравнений, состоящую: а) из двух; б) из трех; в) из четырех уравнений, - для которых совокупность столбцов

является ее фундаментальной совокупностью решений.