Вычисление определителя

В основу метода вычисление определителя положены следующие факты:

а)Определитель треугольной матрицы равен произведению диагональных элементов.

б)Элементарные преобразования второго типа не меняют величины определителя.

Идея метода - используя преобразования второго типа привести матрицу к треугольному виду. Осуществить это можно по следующей схеме:

Умножая первую строку на некоторое число и вычитая из другой строки, обнулить, т.е. сделать равным нулю элементы первого столбца. Напомним, что при вычитании строк вычитаются соответствующие элементы , поэтому А΄-lАЫа₂₁-lа₂₁, а₂₂-lа₁₂… а_2n-lа_1n

Потребуем, чтобы а₂₁-lа₂₁=0Юl=а₂₁ /а₁₁ , чтобы a₃₁=0 Ю a₃₁-l¢a₁₁=0Юl¢= a₃₁/ a₁₁ и т.д. Получим матрицу вида:

Теперь обнулим элементы второго столбца, лежащие ниже главной диагонали. Это нужно сделать второй строкой матрицы , т.к. использование первой строки испортит элементы первого столбца. Определяя l из условия

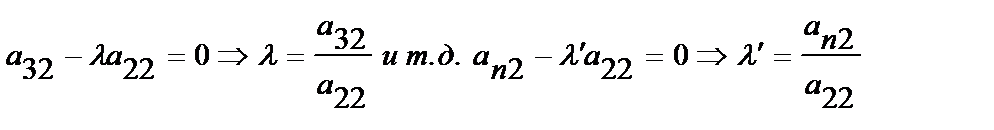
Получим матрицу

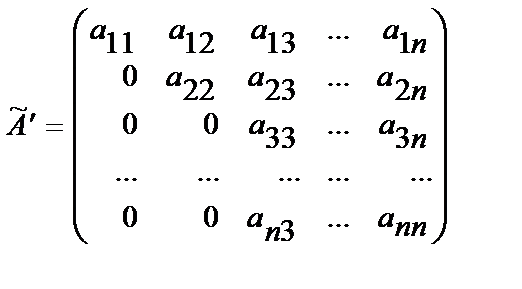
Затем обнулим элементы третьего столбца и т.д. Для обнуления i-го столбца элемент должен быть отличен от нуля т.к.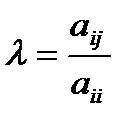

Пример 3.2.1: Вычислить определитель матрицы A.

Решение: Приведем матрицу к треугольному виду:

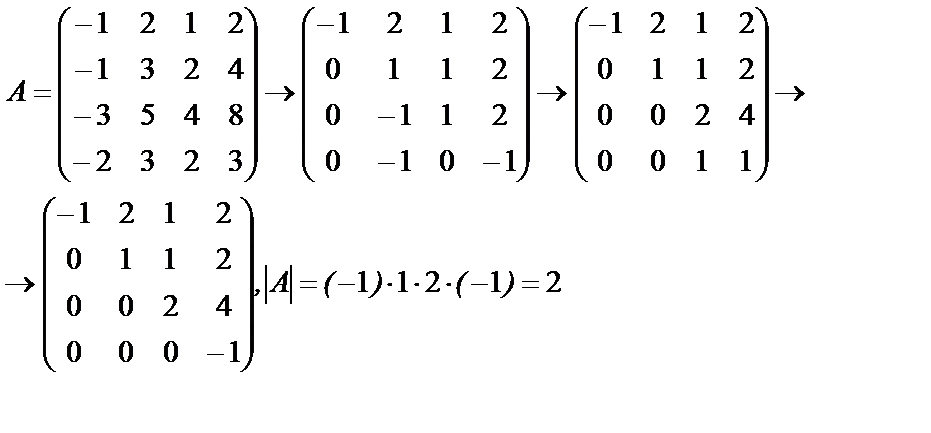
Такой способ вычисления определителя гораздо экономичнее, поскольку число операций не n! , а только n² .

Замечание

При вычислении определителя можно пользоваться и элементарными преобразованиями типа 1) и 3) надо только помнить, как при этом меняется определитель.