Определение 3.1.1.
Элементарным преобразованием матриц называется :
1)умножение строки (столбца) матрицы на число не равное нулю;
2) прибавление к строке (столбцу) матрицы другой строки(столбца), умноженной на произвольное число;
3)перестановка местами двух строк(столбцов) матрицы .
Теорема 3.1.1.
Любое элементарное преобразование, производимое над строками матрицы А, эквивалентно умножению матрицы А слева на матрицу, полученную из единичной матрицы с помощью того же самого преобразования. AnxmЮInxn
Теорема 3.1.2.
Любое элементарное преобразование, производимое над столбцами матрицы А, эквивалентно умножению матрицы А справа на матрицу , полученную из единичной матрицы с помощью того же самого преобразования. AnxmЮImxm
Доказательство этих теорем основано на правиле перемножения двух матриц.
Рассмотрим преобразования, указанные в теореме 3.1.1. на матрице А3x4
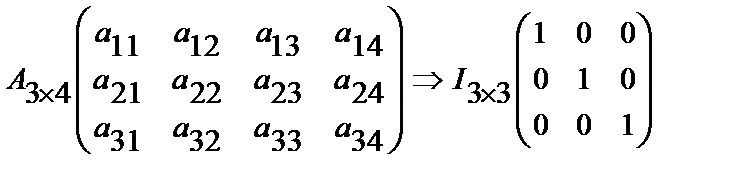
1)Умножим вторую сторону на 
матрица элементарного преобразования 
есть
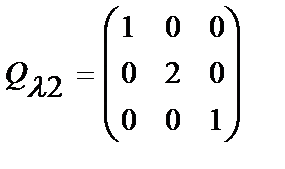
Действительно:
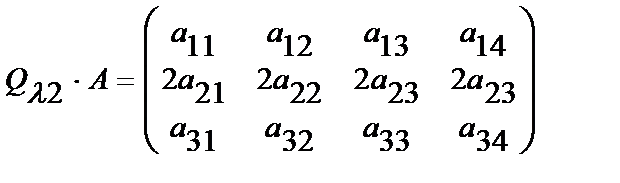
2)прибавим теперь к третей строке первую, умноженную на lЮ матрица элементарного преобразования есть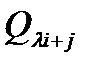 
или:
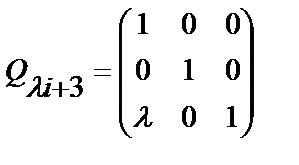
Распишем для нашего случая (A3x4) :
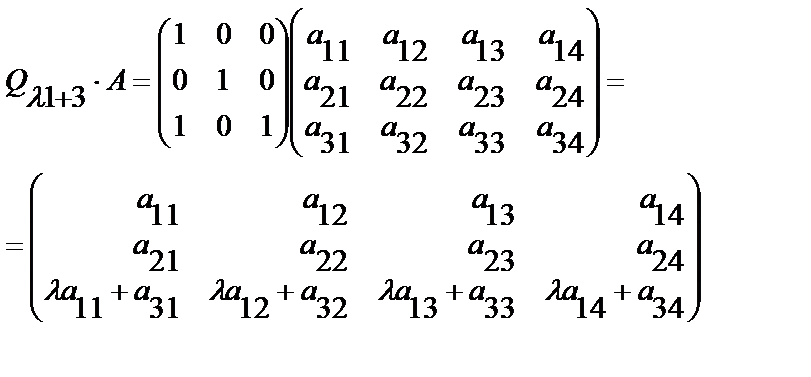
3)переставим первую и третью строки Ю матрицы элем.преобразования Qij
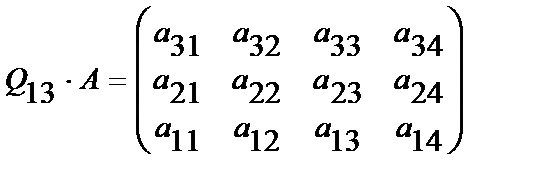
Аналогично можно убедиться в справедливости Теоремы 3.1.2.
Теорема 3.1.3.
Матрица любого элементарного преобразования не вырожденна
Теорема 3.1.4.
Элементарные преобразования не меняют ранга матрицы .
