Определение 2.4.1.
Система линейных уравнений называется однородной , если все элементы правой части системы равны нулю, т.е. если А×X=0
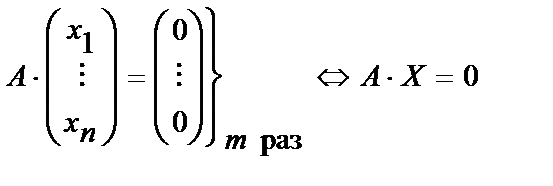
Очевидно , что однородная система всегда имеет тривиальное решение х1=0 xn=0 и следовательно , всегда совместна .
Действительно:
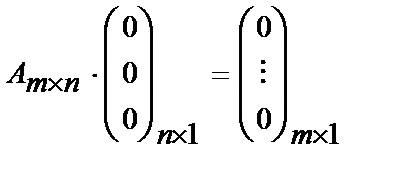
Этот же вывод можно сделать из теоремы Кронекера-Капелли,
т .к. не трудно догадаться , что r(A)= r(A/В)
1) если r(A)=n , то система имеет только единственное решение т.е. тривиальное решение становится единственным, и обратно, если тривиальное решение единственно, то r(A)=n.
2) Однородная система имеет нетривиальное решение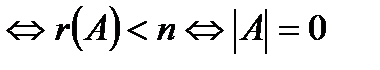 
(т.е. бесчисленное множество решений).
Пример 2.4.1 Решить систему:
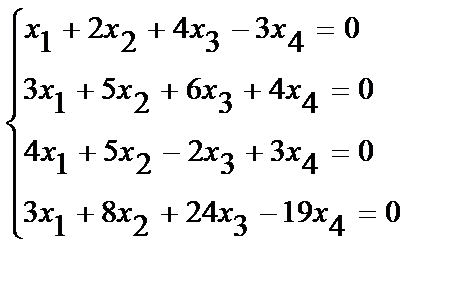
Решение: Найдем ранг основной матрицы системы (суть способа поясним ниже)
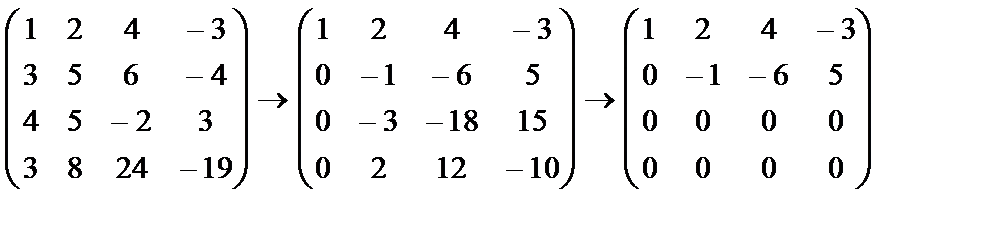
rang=2, r<n, 3-2=1 выберем минор второго порядка не равный нулю:
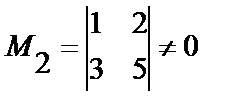
Укороченная система имеет вид :
x1 x2 – базисные, коэффициенты при которых вошли в базисный минор
тогда x3 и x4 - свободные неизвестные, придадим им значения С1иС2 , найдем x1 и x2
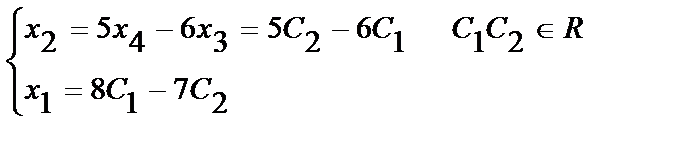
Множество решений системы имеет вид:
