Определение 2.2.1.
Система линейных уравнений называется крамеровской , если основная матрица системы квадратная и невырожденная, т.е. Аnxn , 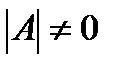
Теорема 2.2.1.
Крамеровская система совместна и имеет единственное решение.
Доказательство:
Аnxn , 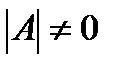 , то для А$ А-1 Используем запись А×X=в Ы А-1×А×х=
, то для А$ А-1 Используем запись А×X=в Ы А-1×А×х=
А-1×вЮI×X = А-1×в Ю X = А-1×в
Докажем единственность решения.
Пусть х и у два решения Ю Аx=в и Ау=вЮ Ах= АуЮ А-1×А×х=
А-1×А×уЮх=у
Доказывая теорему мы получили способ решения системы который называется матричным. Из него можно получить формулы Крамера
Поскольку :
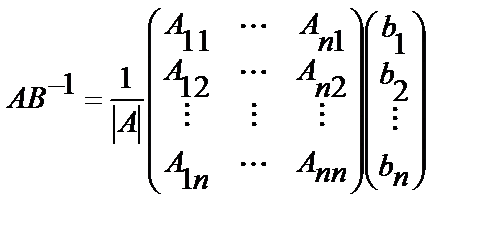 Ю
Ю 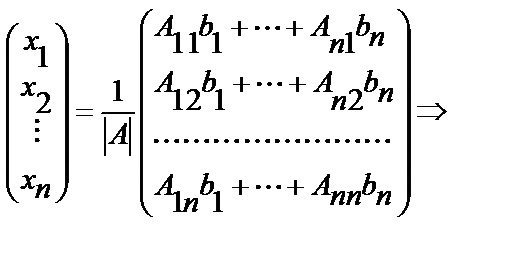

 (2.2)
(2.2)
Di - определитель, полученный из определителя матрицы A заменой i столбца столбцом свободных членов системы.
Di-можно получить используя разложения по i-му столбцу .

Формулы 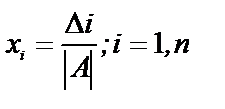 называются формулами Крамера, они используются для систем небольшого порядка .
называются формулами Крамера, они используются для систем небольшого порядка .
Пример 2.2.1. Решим матричным способом систему:
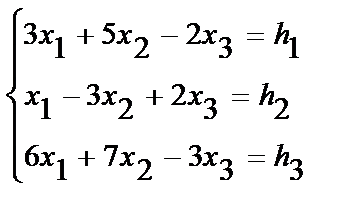
 Решение: Вычислим определитель основной матрицы системы
Решение: Вычислим определитель основной матрицы системы
 detA=10
detA=10 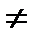 0 Вычислим алгебраические дополнения всех элементов основной матрицы
0 Вычислим алгебраические дополнения всех элементов основной матрицы  ,
, 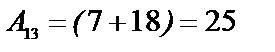
 и т.д.
и т.д.
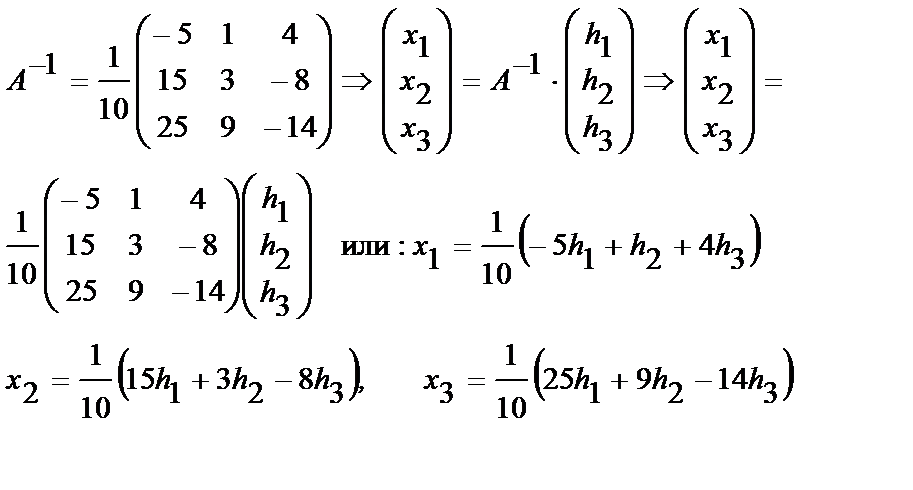
где  - любые действительные числа
- любые действительные числа
Пример 2.2.2. Решить по формулам Крамера систему уравнений:
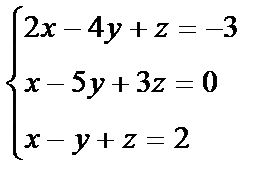
Решение: Вычислим определитель системы:
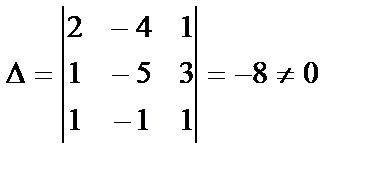
Найдем вспомогательные определители:
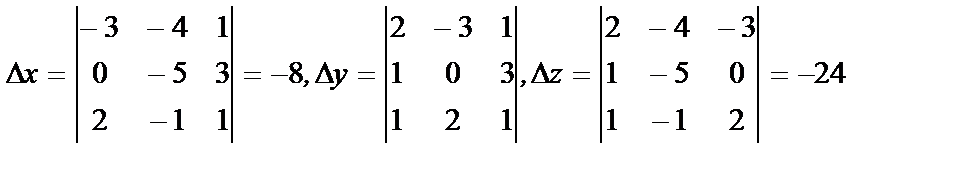
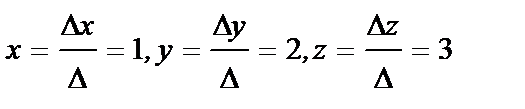
Ответ: {1;2;3}.