По элементам i-й строки:
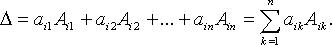
По элементам j-го столбца:
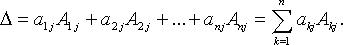
Обратная матрица и свойства
Обра́тная ма́трица — такая матрица A−1, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:
· 
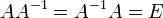
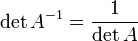, где 
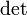обозначает определитель.
· 
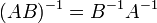для любых двух обратимых матриц 
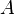и 
.
· 
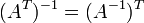где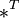 
обозначает транспонированную матрицу.
· 
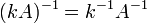для любого коэффициента 
.
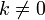Ранг матрицы теорема о базисном миноре
Рангом системы строк (столбцов) матрицы 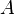с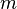 
строк и 
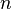столбцов называется максимальное число линейно независимых строк (столбцов).
Теорема.В произвольной матрице А каждый столбец (строка) является линейной комбинацией столбцов (строк), в которых расположен базисный минор
Метод окоймляющих миноров и методом гаусса
При нахождении ранга матрици методом окоймляющих миноров необходимо
переходить от низшего минора к высшему
Ме́тод Га́усса[1] —Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого вида
элеметарные преобразования матриц
Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц.
система линейных уравнений
Система m линейных алгебраических уравнений с n неизвестными
.
