Пусть функция 
имеет конечную производную 
в некотором промежутке 
. Если функция дифференцируема в точке 
, то производная от производной называется второй производной функции 
в указанной точке (или производной второго порядка) и обозначается
.
Так как скорость точки есть производная от пути S по времени 
, ускорение a есть производная от скорости 
, то ускорение является второй производной от пути по времени.
Аналогично, если функция имеет вторую производную в промежутке , то ее производную, конечную или нет, называют третьей производной или производной третьего порядка и обозначают
.
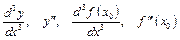