1.Пусть  Определить промежуточное значение
Определить промежуточное значение 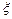 формулы конечных приращений для функции
формулы конечных приращений для функции  на сегменте
на сегменте 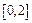 .
.
2.Доказать неравенства: а)  если
если  и
и  б)
б) 
3.Найти на кривой  точку, касательная в которой параллельна хорде, соединяющей точки
точку, касательная в которой параллельна хорде, соединяющей точки 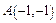 и
и 
4.Верна ли формула конечных приращений для функции 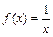 на сегменте
на сегменте  , если
, если 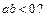
5.Найти функцию такую, что
такую, что ,
,  , если: а)
, если: а) 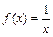 ;
;
б) 
 в)
в)  г)
г) 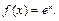
6.Пусть функция  имеет непрерывную производную в интервале
имеет непрерывную производную в интервале  . Можно ли для всякой точки
. Можно ли для всякой точки  указать две другие точки
указать две другие точки  и
и  из этого интервала такие, что
из этого интервала такие, что

 ?
?
Рассмотреть пример: 
 , где
, где 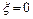 .
.
7.Доказать, что если функция  дифференцируема, но не ограничена на конечном интервале
дифференцируема, но не ограничена на конечном интервале  , то её производная
, то её производная  также не ограничена на интервале
также не ограничена на интервале  . Обратная теорема неверна (построить пример).
. Обратная теорема неверна (построить пример).
8.Показать, что для функции 
 и
и 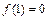 существует конечный предел
существует конечный предел  , однако функция
, однако функция  не имеет односторонних производных
не имеет односторонних производных  и
и  . Дать геометрическую иллюстрацию этого факта.
. Дать геометрическую иллюстрацию этого факта.
9.Доказать неравенства: а)  ,
,  б)
б) 

10.Доказать неравенства: а) 
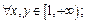
б) 
