1). Смешанное произведение трех векторов равно нулю, если:
а). Хоть один из перемножаемых векторов равен нулю.
б). Два из перемножаемых векторов коллинеарны.
в). Три ненулевых вектора параллельны одной и той же плоскости.
2). Смешанное произведение не изменится, если в нем поменять местами знаки векторного произведения (×) и скалярного (·) умножения.
3). Смешанное произведение не изменится, если переставлять перемножаемые векторы в круговом порядке  ·
· 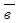 ·
·  =
= 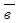 ·
·  ·
·  =
=  ·
·  ·
· 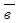
4). При перестановке любых двух векторов смешанное произведение меняет только знак:  ·
· 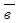 ·
·  = -
= -  ·
· 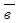 ·
· 
5). Необходимым и достаточным условием компланарности трех векторов служит условие равенства нулю их смешанного произведения, т. е.  ·
· 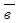 ·
·  = 0.
= 0.