Пусть 
- единичные векторы осей координат, т.е. 
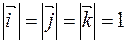и каждый из них одинаково направлен с координатными осями. Тройка векторов называется координатным базисом.
Теорема. Любой вектор пространства можно разложить по базису 
,т.е. представить в виде 
, где 
- некоторые числа (буквы:
- «мю», 
- «ню»).
Это разложение единственное.
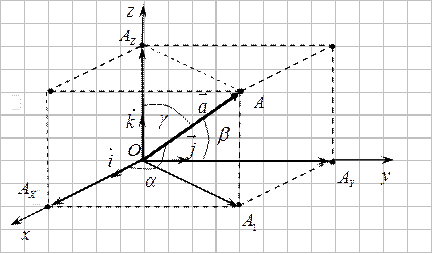
q Доказательство. Приложим вектор 
к началу координат, обозначим его конец 
.Проведем через точку плоскости, перпендикулярные осям координат. Пусть 
, 
, 
-точки пересечения этих плоскостей с осями координат.
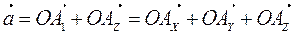
Существует единственная тройка чисел 
, 
, 
таких, что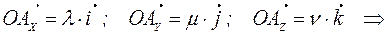 
n.
Формула 
называется разложением вектора по координатному базису.
Числа , , -называются координатами вектора 
, т.е. координаты вектора есть его проекции на соответствующие координатные оси. В символическом виде записывают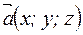 
.
Например, если
,то его координаты 
.
Зная координаты вектора , длину его можно найти по формуле
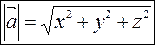
Если известны координаты точек 
и 
, то координаты вектора равны: 
.
Пусть углы вектора с осями 
, 
, 
соответственно равны 
, 
, 
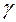. Числа 
, 
, 
называются направляющими косинусами вектора .
; 
; 
;
- основное свойство направляющих косинусов вектора.
