1. Умножение вектора на число. Произведением вектора  на число
на число называется вектор
называется вектор  , который имеет длину
, который имеет длину  , коллинеарен вектору
, коллинеарен вектору  , имеет направление вектора
, имеет направление вектора  , если
, если  , и противоположное направление, если
, и противоположное направление, если  .
.
Например, если дан вектор  , то векторы
, то векторы 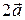 и
и  будут иметь вид:
будут иметь вид:

 2. Сложение векторов. Пусть даны произвольные векторы
2. Сложение векторов. Пусть даны произвольные векторы  и
и  .Сумму векторов можно построить по правилу треугольника и по правилу параллелограмма.
.Сумму векторов можно построить по правилу треугольника и по правилу параллелограмма.
3. Вычитание векторов  можно заменить сложением вектора
можно заменить сложением вектора  с вектором, противоположным вектору
с вектором, противоположным вектору  .
.

4. Свойства линейных операций.
1) 
| - переместительное свойство
сложения;
|
2) 
| - сочетательное свойство сложения;
|
3) 
| - сочетательное свойство умножения
на число;
|
4) 
| - распределительное свойство
относительно суммы чисел;
|
5) 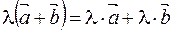
| - распределительное свойство
относительно суммы векторов.
|