Определение. Пусть А – множество элементов произвольной природы, V – действительное линейное пространство. А называется аффинным пространством, связанным с линейным пространством V, если задан закон, по которому каждой паре элементов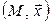 
, где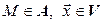 
, ставится в соответствие элемент 
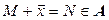, причем выполняются две аксиомы.
1*.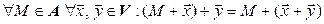 
(рис. 3.1).
2*.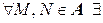 
единственный 
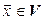такой, что 
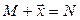. Этот вектор обозначается 
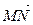. Таким образом, 
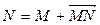(рис. 3.2).
Элементы аффинного пространства называются точками, а операция в аффинном пространстве называется откладыванием вектора от точки.
Рис. 3.1 Рис. 3.2
Как видим, аксиомы аффинного пространства просто «списаны» со школьного точечного трехмерного пространства.
