В дальнейшем будем рассматривать многочлены от переменной, принимающей только действительные значения. Поэтому эту переменную будем обозначать х а не z. Кроме того, все коэффициенты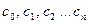 
будем считать вещественными числами.
.
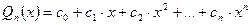Если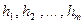 
‑ различные корни многочлена (они могут быть как вещественными, так и комплексными), тогда
,
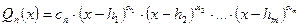где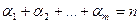 
.
Теорема 1. Если комплексное число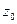 
является корнем многочлена с действительными коэффициентами 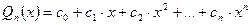, то сопряжённое комплексное число 
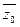также является корнем.
Доказательство.
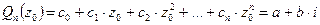, где 
.
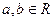Так как 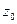‑ корень многочлена, то 
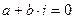, следовательно, 
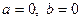. Найдем аналогично значение 
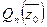. Так как все коэффициенты 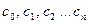‑ действительные числа, то
,
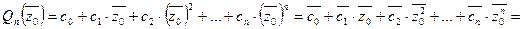
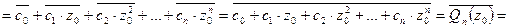
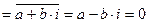так как 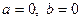. Мы получили, что 
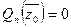, поэтому 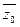‑ корень многочлена 
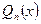. ÿ
Отметим, что если комплексное число 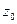является корнем кратности 
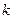, то сопряженное комплексное число 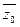также является корнем кратности .
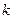Пусть 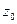и 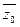‑ пара комплексно сопряжённых корней многочлена 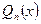, тогда 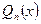делится на 
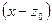и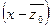 
, следовательно, 
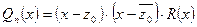. А это значит, что 
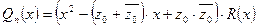. Учитывая, что 
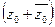и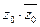 
‑ действительные числа, видим, что 
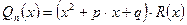. Таким образом, если 
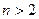, то многочлен 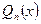делится на многочлен второй степени с действительными коэффициентами.
Теорема 2. Каждый многочлен 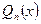с действительными коэффициентами единственным образом разлагается над полем 
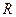действительных чисел в произведение линейных множителей и квадратных трехчленов:
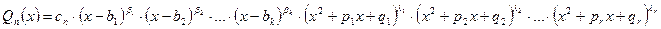
где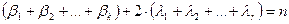 
.
