Любой многочлен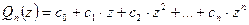 
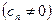степени 
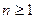над полем комплексных чисел имеет хотя бы один корень.
С помощью этой теоремы и утверждения 1 устанавливается следующий результат.
Утверждение 2.Любой алгебраический многочлен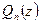 
степени 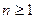имеет ровно п комплексных корней 
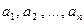и с помощью этих корней представляется в виде
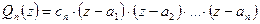. (4)
Доказательство. Так как степень многочлена 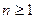, то по основной теореме алгебры у 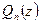существует хотя бы один комплексный корень 
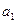. В силу утверждения 1 справедливо представление
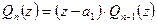
в котором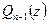 
‑ многочлен степени 
с коэффициентом при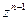 
равным 
.
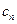Если (т.е.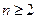 
), то по основной теореме алгебры у многочлена 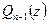существует корень 
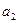. Из утверждения 1 имеем:
.
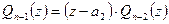Повторяя указанные рассуждения, при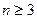 
, 
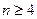, … получим:
,
,
…………………………..
,
.
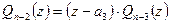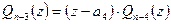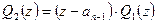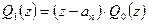В этих представлениях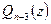 
, 
, …, 
, 
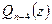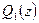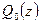‑ многочлены степеней 
, 
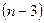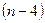, …, 0 соответственно, у каждого из которых коэффициент при старшей степени равен 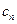. Следовательно, 
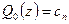. Подставляя вместо 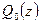значение 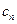в равенство полученное для 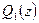, имеем 
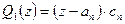. Теперь, подставляя значение 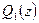в равенство полученное для 
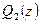, найдем 
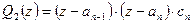. Продолжая процесс получим 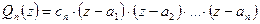. ÿ
Корни 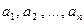многочлена 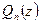могут совпадать между собой. Обозначим 
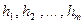‑ различные корни многочлена 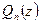. Тогда выражение (4) можно переписать следующим образом:
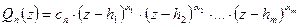, (5)
где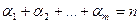 
.
Так как 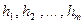‑ различные комплексные числа, то говорят, что 
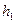‑ корень 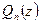кратности 
, 
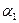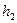‑ корень 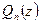кратности 
, …., 
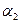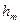‑ корень 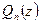кратности 
.
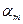