Определение. Пусть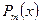 
и 
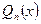многочлены степени т и п.
Если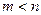 
, то функцию 
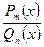называют правильной рациональной дробью.
Если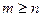 
, то функцию 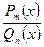называют неправильной рациональной дробью.
Если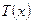 
‑ частное, а 
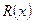‑ остаток от деления многочлена 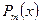на многочлен 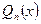, то
,
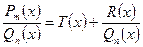где либо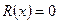 
(в случае, когда многочлен 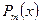нацело делится на многочлен 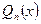), либо 
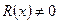, а дробь 
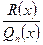является правильной.
I.
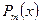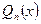Пусть и ‑ многочлены с действительными коэффициентами, 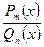‑ правильная дробь, а число 
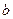‑ действительный корень кратности 
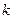многочлена 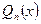. Тогда существуют действительные числа 
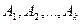такие, что
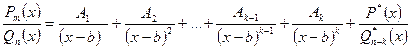
где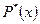 
‑ многочлен с действительными коэффициентами или нуль, 
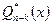‑ частное от деления 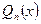на 
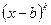при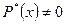 
. Дробь 
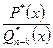является правильной, а числа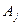 
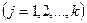и многочлен 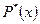определяются однозначно.
II.
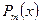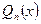Если и ‑ многочлены с действительными коэффициентами, дробь 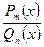является правильной, а число 
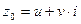где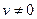 
, ‑ корень кратности 
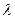многочлена 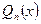, то существуют действительные числа 
, 
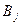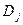
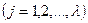и многочлен 
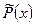с действительными коэффициентами такие, что
,
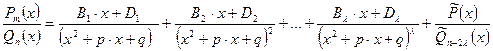где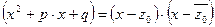 
, 
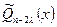‑ частное от деления 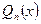на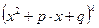 
. Дробь 
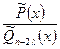при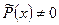 
является правильно, а числа 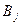и и 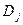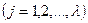многочлен 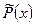определяются однозначно.
III.
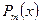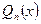Если и ‑ многочлены с действительными коэффициентами, причем 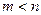, а 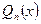представляется в виде:
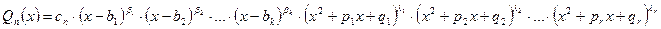
где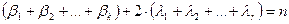 
, тогда
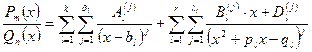
Все коэффициенты в правой части этого выражения ‑ действительные числа и определяются однозначно.
