Теорема (Безу) Остаток от деления многочлена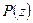 
на двучлен 
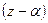равен значению многочлена 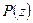при 
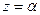, т.е. 
.
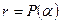Доказательство. Подставив в равенство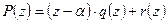 
вместо z значение a, получим 
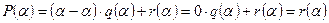, т.е. 
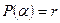. ÿ
Следствие. Многочлен 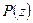делится нацело на двучлен 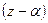тогда и только тогда, когда 
.
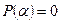Доказательство.
Необходимость. Пусть 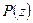делится нацело на 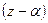. Это означает, что остаток 
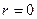. По теореме Безу 
.
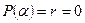Достаточность. Пусть 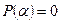, тогда по теореме Безу 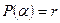, следовательно, 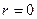, т.е. 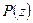делится нацело на двучлен 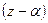. ÿ
Определение. Комплексное число a называется корнем алгебраического многочлена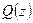 
, если 
.
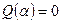Утверждение 1. Если комплексное число a является корнем многочлена ненулевой степени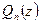 
, то для 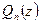справедливо представление
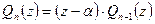(3)
в котором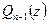 
‑ алгебраический многочлен степени 
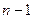, причем коэффициент при 
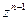у многочлена 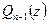совпадает с коэффициентом при 
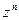у многочлена .
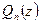Доказательство. Так как a ‑ корень многочлена 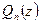, то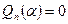 
, т.е. 
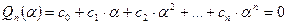. Вычислим разность 
:
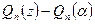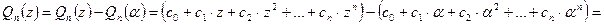
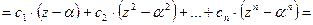
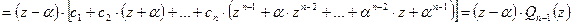
Итак,
,
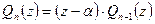где
.
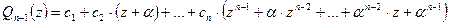Многочлен 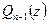имеет степень 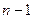и коэффициент при 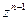равен 
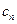.ÿ
Возникает вопрос: всякий ли многочлен имеет корень? Ответ на этот вопрос дает
основная теорема алгебры, которую примем без доказательства.
