Пусть в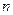 
– мерном линейном пространстве 
выбраны два базиса 
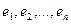и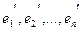 
. Возьмём произвольный вектор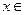 
и разложим его по каждому из выбранных базисов:
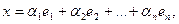(1)
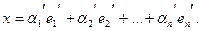(2)
Каждый из векторов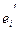 
разложим по базису :
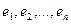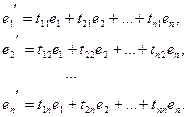(3)
Матрица
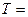
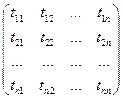
называется матрицей перехода от базиса (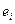 
) к базису ( 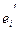). В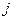 
-ом столбце этой матрицы расположены координаты вектора 
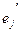в базисе 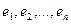. Подставим формулы (3) в равенство (2):
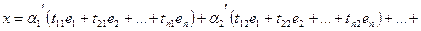
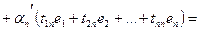
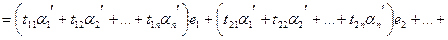
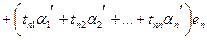(4)
Но каждый вектор можно единственным образом разложить по базису 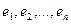. Поэтому из формул (1) и (4) следует, что
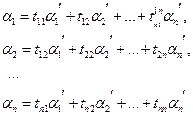(5)
или
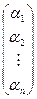
. (6)
Матрица перехода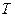 
невырождена (это следует из того, что обе системы 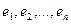и 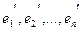- линейно независимы). Умножив обе части равенства (6) на 
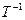, получаем :
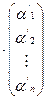
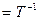
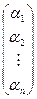. (7)
Формула (7) выражает координаты вектора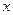 
в базисе ( 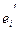), через координаты того же вектора 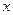в исходном базисе ( ).
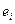Пример. Пусть в пространстве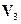 
, выбраны два базиса:
, 
, 
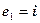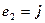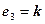
и
, 
, 
.
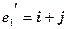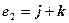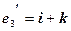Найти координаты вектора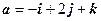 
в базисе 
.
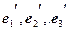Матрица перехода 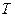от базиса 
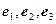к базису 
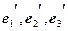имеет вид:
,
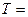
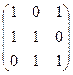так как
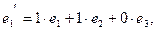
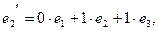
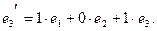
Обратная матрица:
.
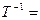
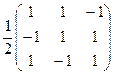По формуле (7):
= 
= 
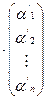
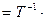
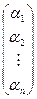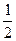
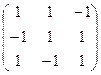
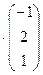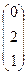
Ответ: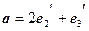 
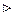
Замечание. Этот пример можно решить другим способом, определив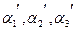 
из равенства:
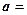
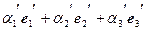
Действительно, отсюда следует, что
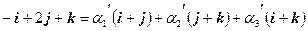
и решив систему
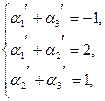
находим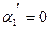 
, 
, 
.
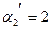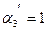