Утверждение. Пусть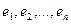 
- базис 
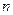- мерного пространства 
.
Тогда для любого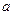 
из существуют числа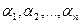 
такие, что
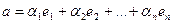(1)
Числа 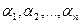в разложении (1) по данному 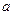определяются однозначно (и называются координатами вектора 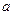в базисе ).
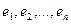1. Существование. Так как 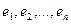– базис пространства , то система векторов 
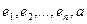– линейно зависима. Следовательно, существует набор чисел 
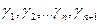, среди которых есть хотя бы одно, не равное нулю, такой что:
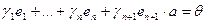(2)
В этом равенстве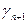 
не равно нулю (т.к. иначе система 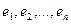была бы линейно зависимой). Из формулы (2) следует равенство :
,
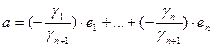т. е. получилась формула (1) с коэффициентами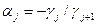 
.
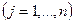2. Единственность. Предположим, что кроме (1) для 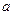имеется разложение:
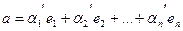(3)
После вычитания из (1) и (3) получаем:
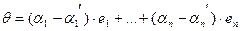
Отсюда, так как система 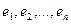– линейно независима следует, что 
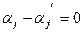,т.е.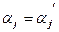 
.
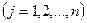