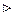Пусть 
- линейное пространство и 
.
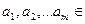
Утверждение 1. Система векторов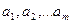 
- линейно зависима в тогда и только тогда, когда один из векторов этой системы является линейной комбинацией остальных.
1. Предположим, что система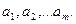 
- линейно зависима. Тогда существуют числа 
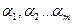, среди которых есть ненулевое, такие, что
.
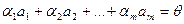Пусть для определенности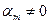 
, тогда из формулы
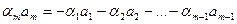
после умножения на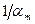 
получим
,
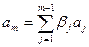где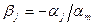 
.
2. Предположим, что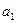 
- есть линейная комбинация векторов 
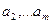, т.е. 
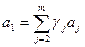, где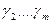 
- некоторые числа. Тогда
.
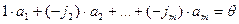Значит, система 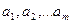- линейно зависима .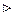 
Утверждение 2. Система векторов 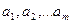- линейно зависима в тогда и только тогда, когда в пространстве существует вектор, который можно представить в виде линейной комбинации векторов 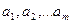, по меньшей мере двумя способами.
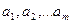1. Если система линейно зависима, то нулевой вектор 
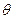можно представить в виде линейной комбинации векторов двумя способами:
1) тривиальный способ:
;
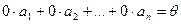2) по определению линейно зависимой системы:
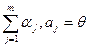, где 
.
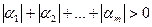2. Предположим, что для некоторого вектора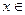 
существуют два различных набора чисел 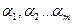и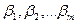 
таких, что 
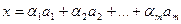и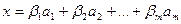 
. Тогда
,
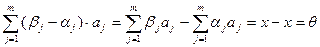где найдется номер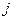 
такой, что 
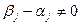. Следовательно, система 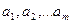-линейно зависима.
