Система векторов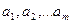 
линейного пространства 
называется линейно независимой системой, если выполнено условие:
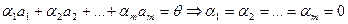. (1)
Читается: из того, что линейная комбинация векторов 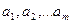равна нулевому вектору, следует, что все коэффициенты этой линейной комбинации равны нулю.
Иначе говоря, система векторов 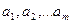является линейно независимой в пространстве , если равенство 
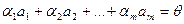выполнено только в том случае, когда 
.
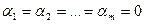Система векторов 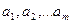называется линейно зависимой в пространстве , если существует набор действительных чисел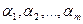 
такой, что выполнены два условия:
1. 
.
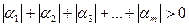2. .
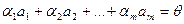Первое из этих условий означает, что среди чисел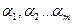 
есть хотя бы одно отличное от нуля.
Пример 1. Система векторов
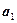
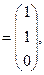
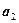
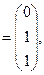
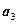
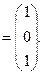
линейно независима в пространстве R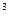 
. Действительно, равенство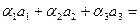 
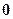эквивалентно системе:
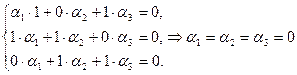, т.к. 
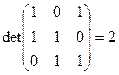, а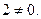 
Пример 2. Докажем, что система функций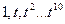 
линейно независима в пространстве 
.
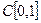Для данных функций и любых чисел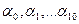 
составим линейную комбинацию: 
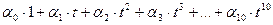равенство этой линейной комбинации нулевому элементу пространства 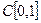эквивалентно тому, что 
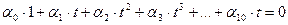для всех 
(*)
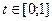Выберем произвольно на [0;1] попарно различные точки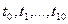 
. Можно считать, что 
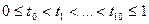. Из условия (*) следует, что
(**)
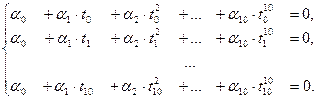Определитель системы (**):
.
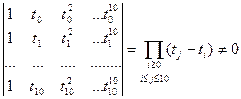Таким образом, условие (*) выполнено только в случае, когда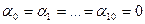 
.
Замечание. Система функций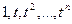 
линейно независима в пространстве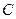 
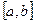(проверяется так же, как в предыдущем примере).
