Утверждение 1. В каждом линейном пространстве нулевой вектор только один.
 Если
Если 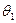 и
и 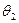 - нулевые элементы линейного пространства
- нулевые элементы линейного пространства  , то
, то
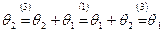
 .
.
Утверждение 2. Для любого вектора 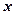 существует только один противоположный элемент.
существует только один противоположный элемент.
 Предположим, что
Предположим, что 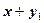
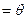 и
и 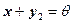 , тогда
, тогда
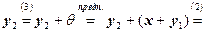
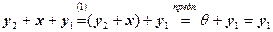
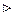 .
.
Элемент противоположный 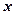 обозначается
обозначается 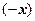 .
.
Утверждение 3. Произведение любого вектора 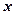 на число
на число 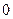 равно нулевому вектору.
равно нулевому вектору.

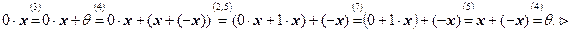
Утверждение 4. Произведение любого вектора 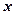 на число
на число 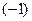 равно вектору, противоположному вектору
равно вектору, противоположному вектору 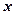 , (т.е.
, (т.е. 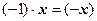 ).
).
 Согласно утверждению 2 достаточно убедиться, что
Согласно утверждению 2 достаточно убедиться, что 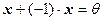 . Имеем:
. Имеем:
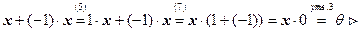 .
.
Утверждение 5. Произведение нулевого вектора 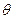 на любое число
на любое число 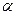 равно
равно 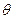 .
.
 Для произвольного вектора
Для произвольного вектора 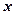 и любого
и любого 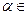 R,имеем:
R,имеем:
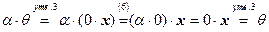
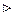 .
.
Следствия:
1. Если 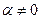 и
и 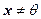 , то
, то 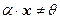 .
.
 Если
Если 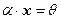 и
и 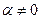 , то
, то 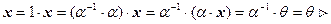 .
.
2. Если 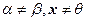 , то
, то 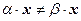 .
.
 Если
Если 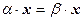 , то
, то 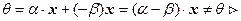 .
.
Пусть 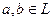 , вектор
, вектор 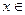
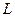 называется разностью векторов
называется разностью векторов 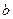 и
и 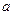 , если
, если 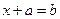 (обозначение:
(обозначение: 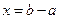 ).
).
Утверждение 6. Для любых элементов 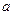 и
и 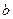 линейного пространства
линейного пространства  разность существует и единственна.
разность существует и единственна.
 (Существование) Для вектора
(Существование) Для вектора 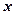
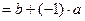 имеем:
имеем: 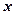
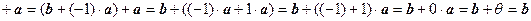 .
.
(Единственность) Предположим, что 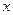
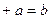 и докажем, что тогда
и докажем, что тогда 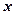
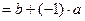 . Имеем:
. Имеем: 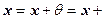
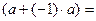
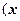
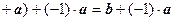
 .
.