Множество 
, состоящее из элементов 
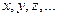, называется линейным пространством, если на этом множестве определены две операции – сложение элементов и умножение элементов на число, удовлетворяющие следующим условиям (аксиомам):
1. 
;
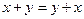2. 
;
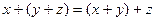3. Существует элемент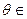 
такой, что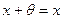 
для любого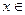 
;
4. Для любого 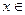существует элемент 
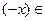
, такой, что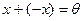 
;
5. 
;
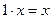6. 
;
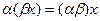7. 
;
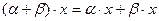8. 
;
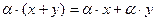Здесь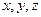 
- произвольные элементы из , 
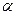и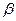 
- произвольные числа.
Условия 1-4 выражают основные свойства операции сложения: коммутативность, ассоциативность, существование нулевого элемента, существование противоположного элемента.
Условия 5 и 6 относятся к операции умножение вектора на число, а условия 7 и 8 связывают между собой две линейные операции. Условие 7 выражает свойство дистрибутивности (или распределительности) для сомножителя из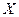 
. Условие 8 – свойство дистрибутивности для числового сомножителя.
Элементы произвольного линейного пространства часто называют векторами, а само линейное пространство часто называют векторным пространством.
Векторы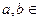 
называются пропорциональными, если один из них получается из второго умножением на некоторое число. В частности, нулевой вектор пропорционален любому вектору.
Примеры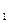: V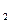 
, V 
, V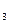 
, 
, 
, 
, 
.
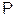
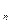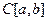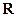
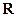
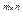Еще одним примером линейного пространства является так называемое нулевое пространство. Это пространство состоит из одного элемента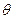 
, а линейные операции определяются формулами: 
, 
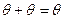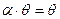
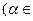R 
.
