Прямая может быть задана как линия пересечения двух плоскостей:
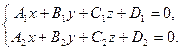(1)
Для того, чтобы от общих уравнений (1) перейти к каноническим уравнениям прямой следует выполнить два шага.
Шаг 1. В качестве направляющего вектора выбрать вектор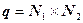 
, где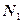 
, 
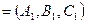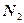
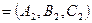- нормальные векторы данных плоскостей.
Шаг 2.Найти точку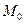 
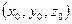,лежащую на линии пересечения двух данных плоскостей. Для этого в уравнения (1) вместо одной из переменных 
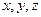следует подставить произвольное значение, а затем найти значения двух других переменных, решив полученную систему.
Пример. Написать канонические уравнения прямой
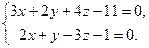(2)
По условию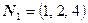 
, 
. В качестве направляющего вектора выберем 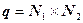. Имеем
,
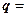
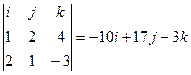т.е.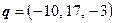 
. Выберем 
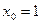, а 
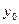и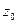 
найдем из системы
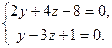
Решением этой системы является пара чисел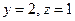 
. Значит, точка 
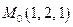лежит на данной прямой и ее канонические уравнения имеют вид:
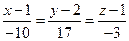. ð
