Пусть в пространстве дана прямая. Ненулевой вектор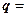 
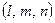, лежащий на прямой или параллельный ей, называется направляющим вектором этой прямой. Заметим, что если 
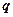- направляющий вектор и число 
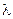не равно 0, то вектор 
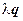тоже направляющий. В частности при 
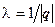получается направляющий вектор единичной длины (орт вектора ).
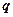Пусть 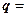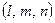- направляющий вектор данной прямой и точка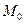 
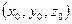лежит на этой прямой. Точка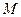 
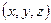лежит на данной прямой тогда и только тогда, когда векторы 
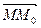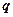и коллинеарны. Отсюда получаются канонические уравнения прямой:
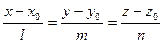. (1)
Равенства (1) означают, что соответствующие координаты векторов 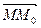и 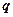пропорциональны. Обозначим через 
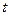каждое из равных отношений в уравнениях (1). И выразим 
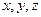через 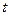. В результате получим параметрические уравнения прямой:
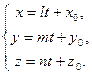(2)
Точка 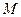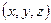лежит на данной прямой тогда и только тогда, когда ее координаты могут быть получены из формул (2) при некотором значении параметра 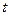. В частности, при 
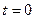точка 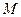совпадает с 
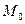. А при изменении параметр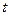а точка 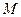перемеща-ется по данной прямой.
Замечание.Формулы (2) раскрывают геометрический смысл уравнений (1) для случая, когда среди чисел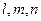 
есть нуль.
