Уравнение плоскости, проходящей через три точки

Пусть точки 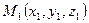, , 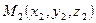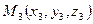не лежат на одной прямой.

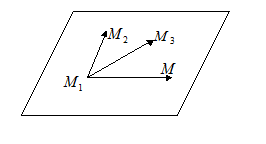
Точка 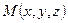лежит в одной плоскости с точками 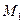, , 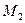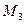тогда и только тогда, когда векторы 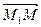, , 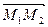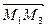компланарны, то есть когда выполнено условие:

.

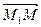
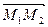
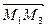
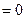Отсюда получаем уравнение:

.

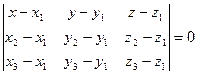Пример. Для точек 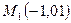, , 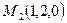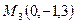имеем

,

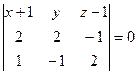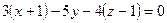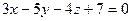т.е. или . ð

Канонические и параметрические уравнения