Взаимное расположение двух плоскостей

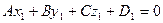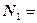
Пусть даны две (различные) плоскости

, и , .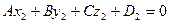

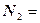
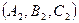Возможны три случая.

I. Плоскости параллельны. В этом случае векторы 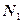и 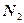коллинеарны и выполнены равенства:

.

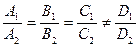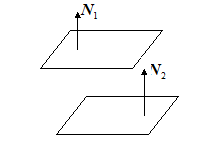
II. Плоскости перпендикулярны. Тогда векторы 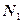и 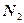ортогональны, то есть 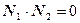или

.

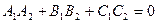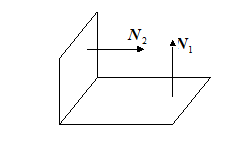
II. 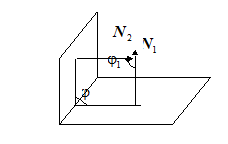Плоскости пересекаются, но не перпендикулярны.

Обозначим через 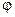линейный угол двугранного угла между данными плоскостями. Нормальные векторы 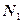и 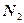можно выбрать так, что 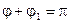, где 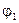- угол между 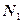и 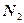. Тогда угол 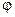находится из равенств

.
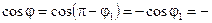
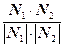