Расстояние от точки до плоскости

Пусть дана плоскость

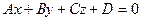(1)

и пусть точка 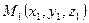не принадлежит этой плоскости. Обозначим через 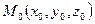ортогональную проекцию точки 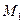на данную плоскость.

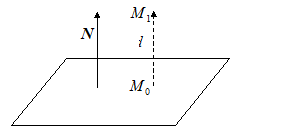
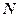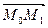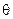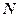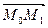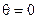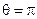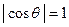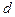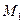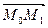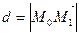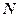
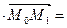
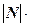
Векторы и коллинеарны, так как они перпендикулярны одной и той же плоскости. Если - угол между и то либо , либо . В обоих случаях . Расстояние от точки до данной плоскости совпадает с модулем вектора : . Поэтому из формулы 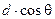получаем

.

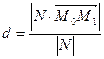Здесь

.

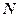
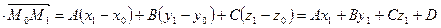Таким образом, расстояние от точки 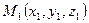до плоскости 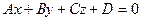вычисляется по формуле

.
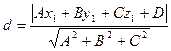