Пусть в системе координат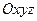 
дана точка 
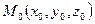и вектор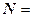 
, 
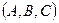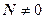. Получим уравнение плоскости, проходящей через точку 
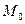перпендикулярновектору 
. 
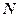Точка 
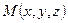лежит на этой плоскости тогда и только тогда, когда векторы
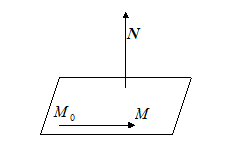
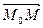и 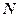ортогональны, т. е. если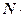 
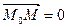. Так как 
,
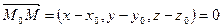то искомое уравнение имеет вид
. 
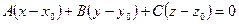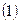
Обозначив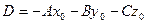 
, из 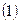получаем общее уравнение плоскости:
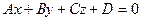
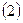
Вектор, перпендикулярный плоскости, называется нормальным вектором этой плоскости. Для плоскости, имеющей уравнение , одним из нормальных векторов является вектор .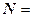 
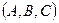Пример. Составим уравнение плоскости, проходящей через точку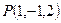 
перпендикулярно вектору 
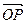. По условию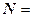 
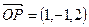является нормальным вектором плоскости и точка 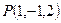лежит на плоскости. Поэтому можно применить уравнение 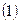, считая 
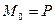. В результате получим уравнение
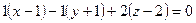
или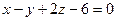 
. ð
