Покажем, как выражаются векторное и смешанное произведения через координаты векторов.
Предложение1. Если
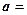
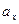
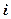
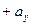
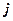
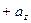
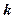 и
и 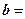
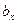
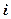
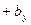
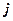
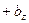
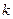 ,
,
то
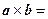
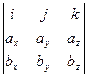 , (1)
, (1)
где правая часть по определению равна
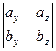
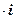
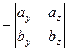
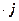
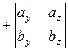
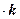 .
.
 Имеем следующую таблицу умножения координатных ортов:
Имеем следующую таблицу умножения координатных ортов:
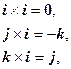
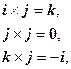
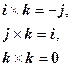
Пользуясь свойствами векторного произведения, получим:
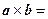 (
( 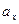
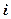
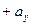
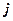
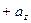
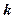 )
) 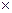 (
( 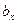
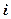
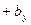
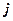
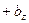
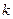 )=
)=
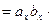
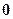
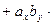
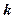
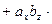
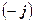
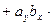
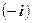
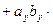
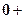
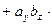
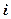
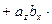
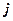
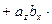
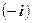

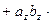
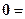
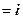
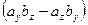
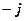
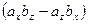
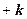
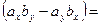
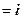
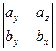
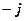
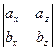
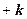
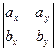 .
. 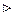
Пример. Даны три точки: 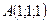 ,
, 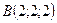 ,
, 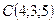 . Найдем площадь S тре-угольника
. Найдем площадь S тре-угольника 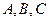 .
. 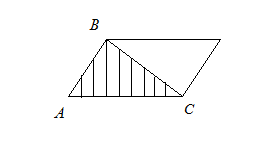 Заметим, что искомая площадь равна половине площади параллелограмма, построенного на векторах
Заметим, что искомая площадь равна половине площади параллелограмма, построенного на векторах 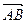 и
и 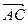 , т.е. верна формула
, т.е. верна формула
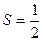
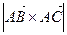 .
.
Так как 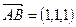 ,
, 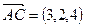 , то
, то
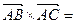
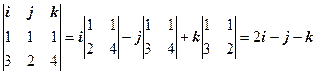
и, значит,
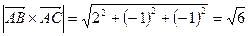 .
.
Ответ: 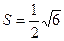 . ð
. ð
Предложение 2. Смешанное произведение векторов
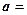
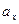
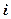
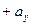
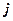
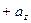
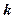 ,
, 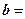
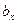
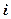
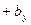
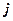
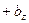
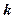 ,
, 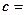
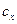
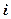
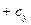
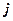
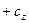
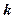
вычисляется по формуле
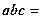
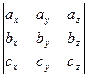 .
.
 По предыдущему утверждению,
По предыдущему утверждению,
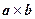
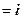
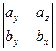
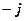
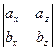
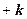
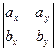 .
.
Следовательно,
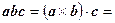
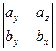
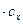
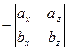
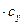
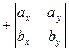
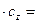
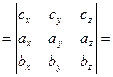
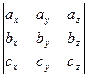 .
. 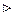
 Пример. Даны точек
Пример. Даны точек 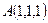 ,
, 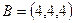 ,
, 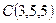 ,
, 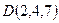 найдем объем
найдем объем 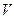 пирамиды
пирамиды 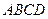 . Искомый объем в 6 раз меньше
. Искомый объем в 6 раз меньше
объема параллелепипеда, построенного на векторах 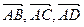 , т.е. верна формула
, т.е. верна формула
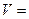
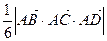 .
.
Имеем: 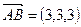 ,
, 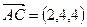 ,
, 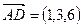 . Следовательно,
. Следовательно,
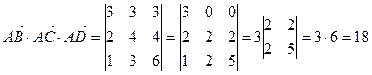 .
.
Ответ: 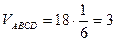 . ð
. ð
Замечание. Из предложения 2 следует, что векторы
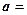
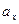
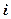
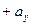
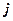
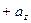
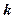 ,
, 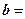
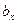
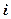
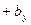
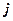
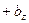
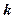 ,
, 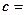
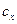
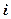
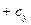
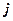
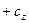
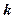 ,
,
компланарны в том и только в том случае, когда
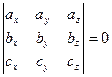 .
.