Пусть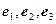 
ортонормированный базис пространства 
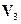и пусть 
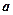и 
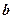- произвольные векторы пространства 
.
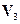Утверждение. Справедлива формула
,
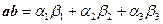где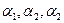 
и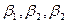 
– координаты векторов 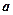и 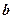в базисе .
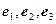По условию,
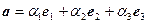и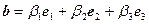 
,
где
, 
.
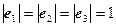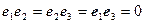Пользуясь свойствами скалярного произведения, получаем
. 
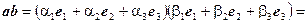
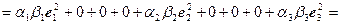
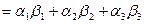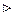
Следствие 1. Если
, 
,
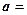
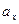
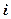
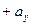
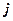
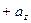
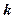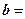
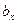
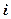
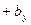
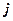
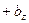
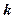то
.
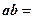
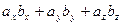Следствие 2 . Есл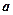и и 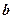ненулевые векторы, то косинус угла меду ними находится по формуле:
.
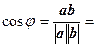
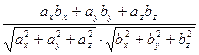Следствие 3. Для того что бы векторы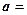 
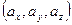и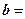 
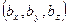были ортогональны, необходимо и достаточно, чтобы
.
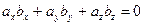Пример. Для точек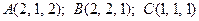 
найдем угол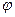 
. 
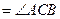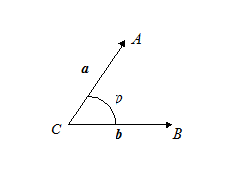Пусть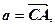 
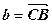. Тогда
, 
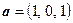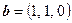
и, следовательно,
, 
.
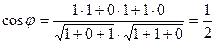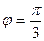Ответ: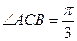 
. ð
