Пусть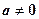 
и 
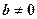. Проекция вектора 
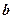на направление вектора 
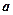определяется равенством
,
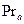
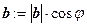где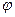 
- угол вежду 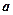и 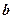. Аналогично,
.
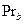
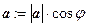Отсюда
= 
.
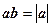
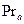
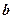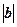
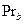
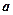В частности,
, 
, 
.
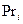
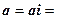
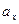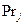
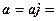
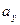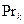
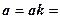
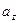Проекция вектора 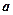на произвольную ось 
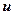- это, по определению, проекция вектора 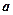на направление орта оси 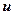. Обозначение: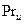 
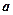. Если 
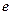– орт оси 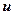, то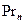 
.
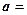
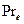
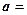
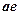Проекция суммы двух векторов на одну и ту же ось равна сумме проекций:
,
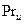
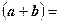
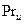
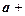
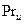
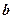так как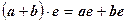 
. Аналогично для конечного числа векторов:
.
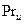
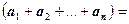
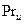
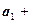
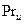
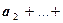
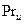
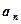Кроме того, для любого числа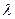 
проекция произведения 
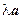равна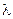 
.
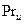
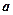Проекция нулевого вектора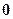 
на направление произвольного ненулевого вектора и на произвольную ось считается равной нулю.
