Нехай дані три довільні вектори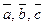 
. Якщо вектор 
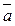векторно помножити на вектор 
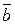, а потім вектор, який отримаємо при цьому 
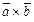скалярно помножити на вектор 
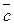, то в результаті отримаємо число 
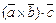, яке називається мішаним добутком векторів 
.
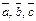Геометричне тлумачення мішаного добутку векторів вказує наступна теорема.
Теорема 6. Мішаний добуток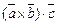 
дорівнює об’ємові паралелепіпеда, побудованого на приведених до спільного початку векторів 
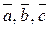, взятих зі знаком „+”, якщо трійка 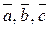– права і зі знаком „–”, якщо трійка 
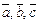ліва. Якщож вектори 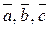компланарні то 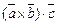дорівнює нулеві.
Припустимо, що вектори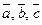 
не компланарні. Тоді 
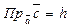з точністю до знака, дорівнює висоті h паралелепіпеда побудованого на зведених до спільного початку векторів 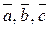при умові, що основою служить паралелограм, побудований на векторах 
.
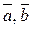Отже його об’єм паралелепіпедаобчислюється за формулою
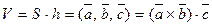(28)
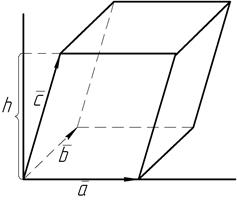
Рис.9
