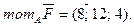Розглянемо задачі в яких при їх розв’язанні застосовується векторний добуток векторів.
Задача 1. Обчислення площі паралелограма: згідно з властивостей площа паралелограма дорівнює добуткові його суміжних сторін на синус кута між ними, тобто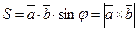 
тому можна вивести формулу для обчислення площі паралелограма:
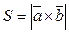(25)
Формула (25) є формулою для обчислення площі паралелограма.
З обчислення площі паралелограма знаходимо формулу обчислення площі трикутника вона буде дорівнювати половині площі паралелограма, тобто
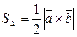(26)
Формула (26) є формулою для обчислення площі трикутника.
Приклад 15. Обчислити площу паралелограма, побудованого на векторах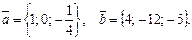 
Розв’язання:
Застосовуючи формулу (25) отримаємо
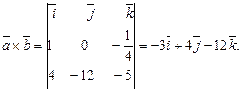
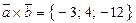Тому площа дорівнює:
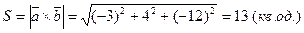
Відповідь:Площа паралелограма дорівнює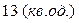 
Приклад 16. Знайти площу трикутника з вершинами у точках А(1; 2; 1), В(4; 3; 2), С(2; 4; 4).
Розв’язання:
Нехай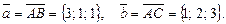 
Знаходимо 
:
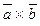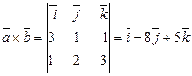
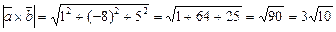
Площа трикутника ΔАВС дорівнює половині площі паралелограма, побудованого на векторах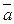 
та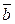 
:
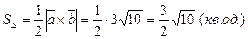
Відповідь:Площа ΔАВС дорівнює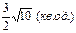 
Задача 2. Обчислення моменту сили.Якщо вектор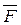 
зображує силу, прикладену до точки М, а вектор 
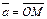, то вектор 
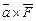є моментом сили 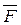відносно точки О, тобто
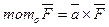(27)
Формула (27) є формулою для обчислення моменту сил.
Приклад 17. Сила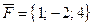 
прикладена до точки М(1; 2; 3). Знайти момент цієї сили відносно точки А(3; 2; -1).
Розв’язання:
Знаходимо координати вектора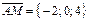 
і застосовуючи формулу (26) отримаємо
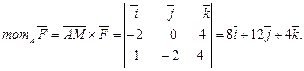
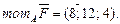
Відповідь:Момент сили дорівнює 
