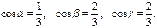Нехай вектор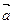 
утворює з координатними осями кути 
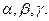Тоді відповідно до (9) маємо:
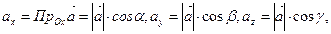або
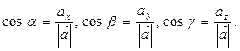(12)
Косинуси кутів, які утворюють вектор з осями координат, називають його напрямними косинусами.
Знайдемо суму квадратів напрямних косинусів вектора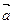
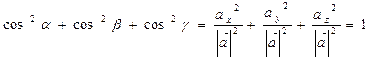
Отже,
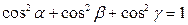. (13)
Із співвідношення (13) випливає, що вектор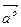 
= 
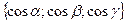є одиничним вектором і має напрям вектора .
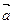Отже, в прямокутній системі координати будь-якого одиничного вектора є його напрямними косинусами.
Приклад 5. Знайти напрямні косинуси вектора =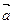 
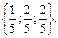
Розв’язання:
Знайдемо довжину вектора :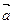 
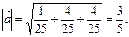Тому згідно з (12)
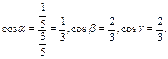
Відповідь: 
