Теорема 3. Если два вектора определены своими декартовыми прямоугольными координатами а={x1,y1,z1}, b={x2,y2,z2},то их скалярное произведение равно сумме попарных произведений их соответствующих координат, т.е.
a·b=x1x2+y1y2+z1z2 (5)
Доказательство. Т.к. базисные векторы являются попарно ортогональными и имеют единичную длину, то: 
.
=12сos 0˚=1,
Учитывая, что а=x1i+y1j+z1k, b= x2i+y2j+z2k,получим
a·b=(x1i+y1j+z1k)(x2i+y2j+z2k)=x1x2+0+0+y1y2+0+0+z1z2=x1x2+y1y2+z1z2. ч.т.д.
При a=bполучаем a·а=|а|2=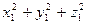 
.
Следствие 1.Векторы а={x1,y1,z1} и b={x2,y2,z2} являются ортогональными тогда и только тогда, когда x1x2+y1y2+z1z2=0.
Пример. Проверить, являются ли ортогональными векторы а=(0;6;-3) и b=(2;4;8). A·b=0·2+6·4+(-3)·8=0
Следствие 2.
Угол между двумя векторами: cos φ= 
. (6)
Пример. Найти угол между векторами а=(1;2;-3) и b=(2;4;0)
cos φ= 
, φ=arccos 1/28
