Если угол между двумя ненулевыми векторами прямой, то такие векторы называются ортогональными.
Теорема 1. Два вектора ортогональны тогда и только тогда, когда их скалярное произведение равно нулю.
Доказательство. Необходимость. Пусть векторы 
и 
ортогональны, j - угол между ними. Тогда cos j=0Þ 
=0.
Достаточность. Пусть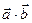 
=0. Докажем, что векторы и ортогональны. Исключим тривиальный случай, когда хотя бы один из векторов или равен 0. Если оба вектора ненулевые, то 
>0, 
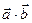>0Þиз равенства =0 и (1) следует, что cos j=0, т.е. векторы и ортогональны. Ч.т.д.
Теорема 2. Два ненулевых вектора и составляют острый (тупой) угол тогда и только тогда, когда их скалярное произведение положительно (отрицательно).
Доказательство. Т.к. векторы и ненулевые, то знак скалярного произведения совпадает со знаком cos j. Если угол j не превосходит p, то cos j положителен тогда и только тогда, когда j - острый угол, и отрицателен тогда и только тогда, когда j - тупой угол. Ч.т.д.
