Пусть балка имеет два состояния:
1) рисунок
2)рисунок
Где ∆12 – перемещение в точке 1 от действия силы, приложенной в точке 2.
∆21 – перемещение в точке 2 от силы, приложенной в точке 1.
Для вывода теоремы сначала балку загружаем силой F1, а затем силой F2
Рисунок
Совершенная работа равна: W=W11+W22+W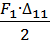12= 
+ 
+ F1∙∆12
Рисунок
W=W22+W11+W21= + + 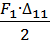F2∙∆21
Т.к. силы одинаковы, то и работа одинакова, из этого следует: F1∙∆12 = F2∙∆21 – теорема о взаимности работ (теорема Бетти): Работа сил первого состояния на перемещение второго состояния равна работе сил второго состояния на перемещение первого состояния.
Если принять F1=F2=1 (безразмерная величина), то получим теорему о взаимности перемещений (теорема Максвелла): δ12=δ21- перемещение от единичной силы. Th: перемещение в точке приложения первой единичной силы по её направлению, вызванной второй единичной силой равно перемещению в точке приложения второй единичной силы по её направлению, вызванной первой единичной силой.
