На рисунке 5.1 показан график переходного процесса для нормированной (приведенной к единичной) функции уn٭ объекта по формуле:
у*n = 
, (5.5)
где n=0,1,2,3 ….
На графике введены следующие обозначения:
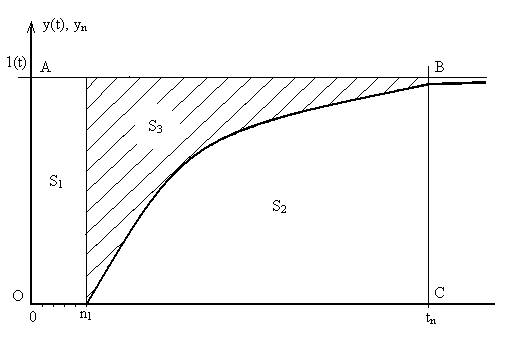
Рис. 5.1. Аппроксимация графика переходного процесса
S1 - площадь на интервале 0-n1, когда у*n=0; S2 - площадь под кривой на интервале от n1 до tn = nTk; S3 - площадь над кривой переходного процесса; ОАВС - прямоугольник, включающий S1,S2, и S3 .
Очевидно, что
S = SОАВС = nTk; (5.6)
S1 = n1Tk . (5.7)
Площадь S2 вычисляется по методу Симпсона. Тогда согласно методике БНТУ
S3 = S- S1- S2= Tм, (5.8)
где Tм - постоянная времени модели объекта.
Для упрощение при вычислении S2 рекомендуется вычисление производить, включая все значения от у*0 до у*n, не забывая, что n = k (количество значений в файле данных).
Согласно методу Симпсона для цифрового интегрирования получим:
S2 = 
(у*0 + 4у*1 + 2у*2 + 4у*3 + …+у*n). (5.9)
Следует помнить, что при интегрировании по этому методу n должно быть четным. Поэтому для использования (5.9) необходимо произвести анализ значения k, например, используя стандартную функцию odd (k): если kнечетное, то надо добавить один элемент в массив файла данных:
уk+1= уk,,
а затем изменить количество элементов массива: 
k=k+1.
Примечание.Вместо (5.9) можно использовать с целью упрощения другую формулу:
S2 = 
(у0 + 4у1 + 2у2 + 4у3 +…+ уn). (5.10)
Здесь нормирование учитывается делением на kм в конце.
